Mois : mars 2019

Influence du vent sur le temps de vol (2): méthode du temps corrigé.

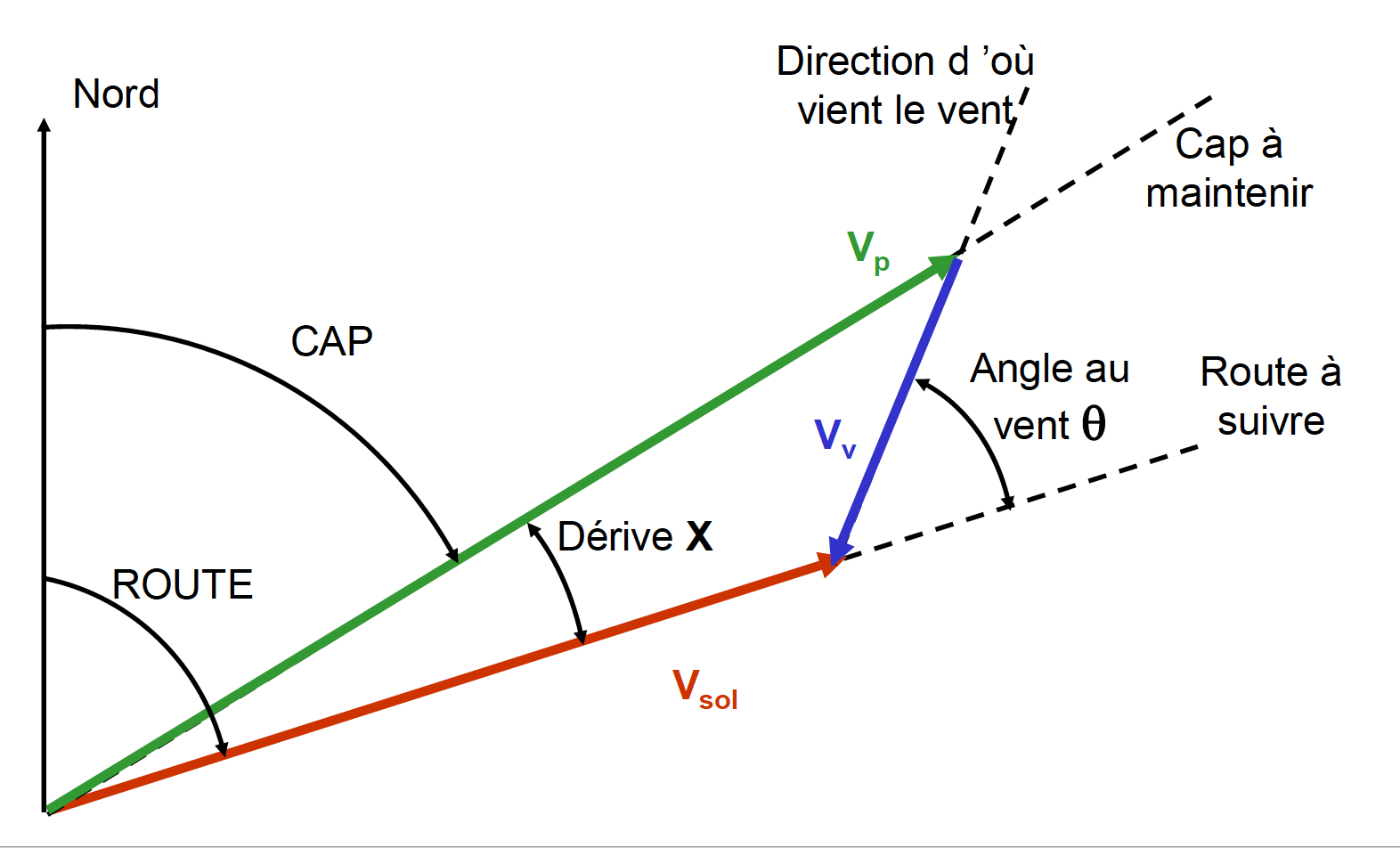
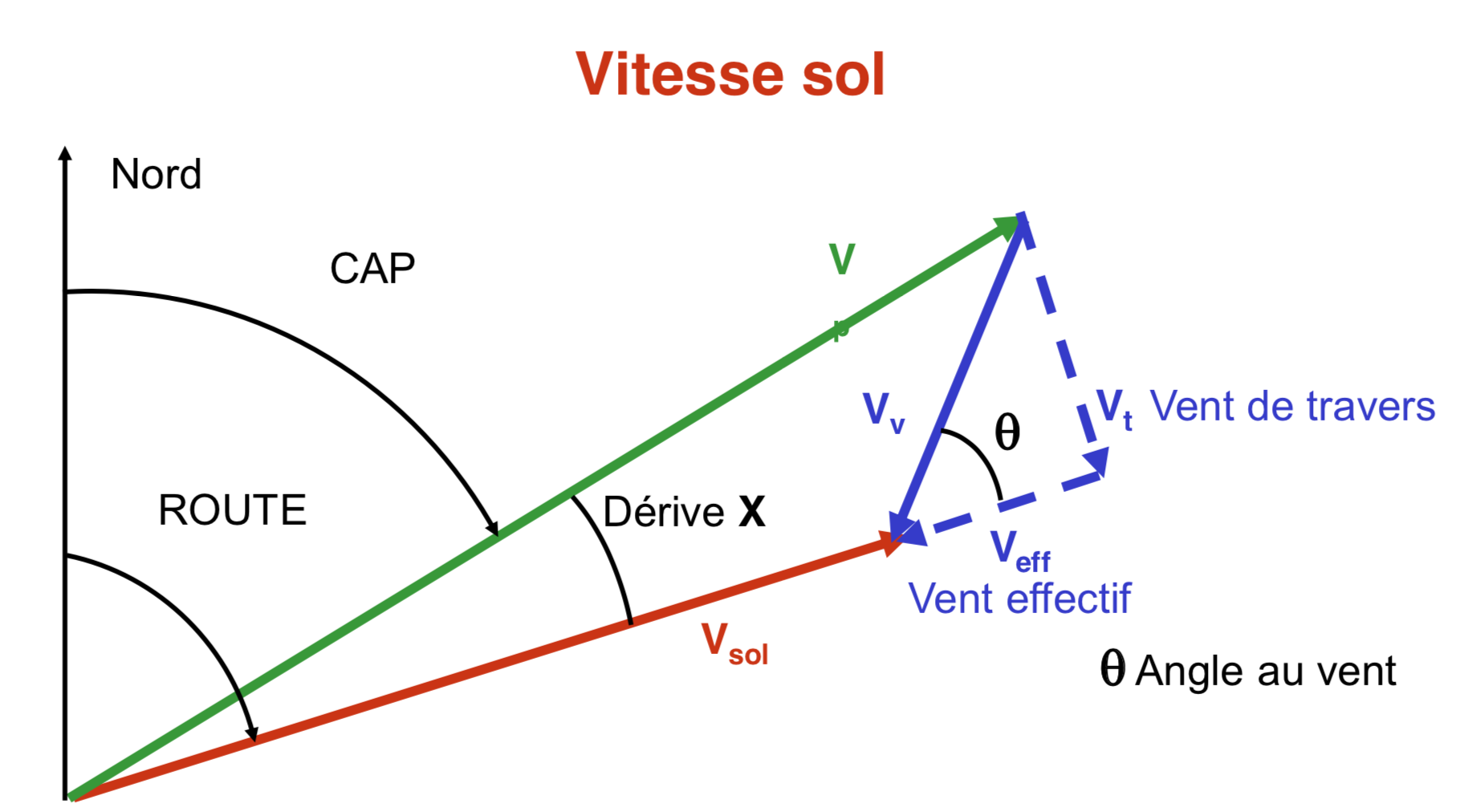
Le temps pour parcourir la distance D à la vitesse Vp s’il n’y a pas de vent, est {\text{T}_{\text{sv}}=\frac{D}{ V_p}}. Le temps pour parcourir la même distance s’il y a du vent de vitesse W, l’angle au vent étant comme à notre habitude noté θ, est {T=\frac{D}{ V_p-W.\cos \theta }} .
Comme à notre habitude, W est toujours positif, θ est plus petit que 90° s’il y a une composante de face, et plus grand s’il y a une composante favorable. On vérifie bien que T est supérieur à Tsv s’il y a une composante de face, c’est à dire si θ<90°.
Dans les manuels, on désigne par t le nombre approximatif de minutes (respectivement de secondes) qu’il faut ajouter au temps sans vent exprimé en heures (respectivement en minutes) pour obtenir le temps en tenant compte du vent. Nous noterons te le nombre exact de minutes (respectivement de secondes). On détermine aisément
{t_e=60.\frac{T-\text{T}_{\text{sv}}}{ \text{T}_{\text{sv}}}}
Développons, en utilisant les notations de notre précédent article relatif au triangle des vitesses
\frac{t_e}{60}={\frac{T-\text{T}_{\text{sv}}}{ \text{T}_{\text{sv}}}}={\frac{\frac{D}{ V_p-W.\cos \theta }-\frac{D}{ V_p}}{ \frac{D}{ V_p}}}= {(\frac{1}{ 1-\frac{W}{ V_p}.\cos \theta }-1)}= {(\frac{1}{ 1-\sin X_m.\cos \theta }-1)}
Sin Xm cos θ étant, en valeur absolue, plus petit que 1 (sauf si la dérive est de 90°, auquel cas te est infini et le calcul est terminé), notre expression peut s’écrire (avec Xm en radians)
{\frac{t_e}{60}=\sum_{n=1}^{\infty} {(\sin X_m.\cos \theta)}^{n}}=X_m.\cos \theta+X_m^2.\cos^2 \theta+X_m^3.(\cos^3 \theta -\frac{\cos \theta}{6})+....
Pour une dérive exprimée en degrés l’expression devient {\frac{3}{\pi} t_e =X_m.\cos \theta+ \frac{\pi}{180} X_m^2.\cos^2 \theta+\frac{\pi^2}{180^2}. X_m^3.(\cos^3 \theta -\frac{\cos \theta}{6})+.... }
Si la dérive max Xm est suffisamment petite, alors tous les termes de la somme deviennent négligeables à l’exception du premier, et l’expression devient, si on arrondi π à 3, te≃Xm cos θ, formule donnée dans tous les manuels. Dans la suite, comme dans les manuels, on pose t=Xm cos θ.
Considérons maintenant qu’il faut aller jusqu’au deuxième terme de la somme, ce qui revient à approcher notre résultat au moyen d’une parabole et non plus d’une droite. En arrondissant π à 3, on obtient:
{t_e\simeq { X_m.\cos \theta}+ {\frac{X_m^2}{60}.\cos ^2\theta}=t+\frac{t^2}{60}}.
On note en général dans les manuels ce deuxième terme t″, et on définit le temps corrigé par
tc=t+t″, avec t=Xm cos θ et t″{=\frac{t^2}{60}}
Exemple: Le vent W est de 30kt, ma vitesse propre Vp est de 120kt, l’angle au vent est 60°. On a cos θ= cos 60°= 0.5
Fb {=\frac{60}{V_p}= \frac{60}{120}= \frac{1}{2}}=0.5
Xm=Fb x W = 0.5 x 30 = 15°
t=Xm cos θ = 15 x 0.5 = 7.5s
t″{=\frac{t^2}{60}= \frac{7.5^2}{60}= \frac{56.25}{60}}=0.9s.
On en déduit qu’avec le vent de face, il faudra ajouter 7.5+0.9= 8.4 minutes par heure (ou secondes par minute) au temps calculé sans vent, et qu’avec le vent dans le dos il faudra retrancher 7.5-0.9=6.6 minutes par heure (ou secondes par minute) au temps calculé sans vent. Ces formules approchées donnent un résultat très voisin de la réalité (dans notre exemple 8.4 et 6.6 pour des valeurs exactes de 8.6 et 6.7), et peuvent être utilisées en calcul mental pour ajuster en fonction du vent vos temps de parcours, que ce soit pour une longue navigation ou au cours d’une attente en hippodrome. En pratique, en calcul mental on arrondi t et tc à la seconde ou minute la plus voisine bien entendu, et on peut même souvent négliger tc.

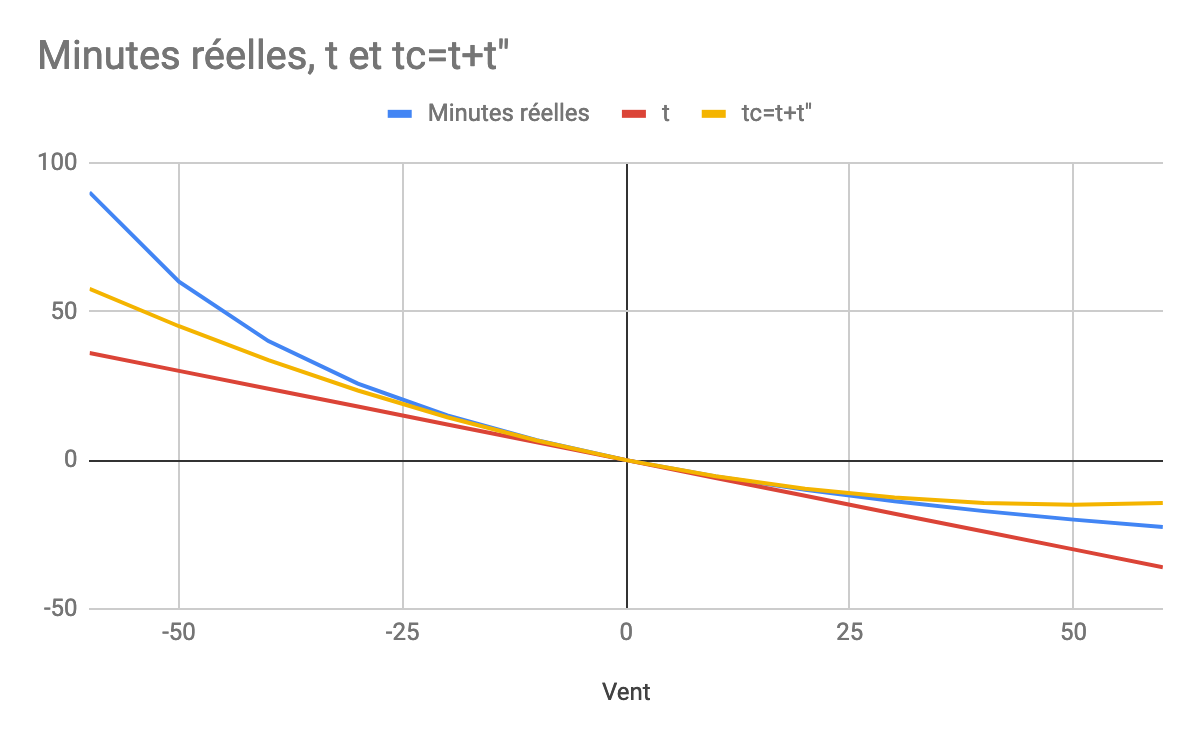
Vous voyez sur le graphique, pour une distance de 100NM à parcourir à la vitesse propre de 100kt, le nombre de minutes à ajouter (partie gauche du graphique avec du vent de face) ou retrancher (partie droite du graphique avec vent de dos) au temps sans vent d’une heure, en fonction du vent pour chacune des méthodes de correction (calcul exact, méthode du t, méthode du temps corrigé). Les résultats sont sans surprise: plus la méthode est facile à mettre en œuvre, moins elle est précise, et plus le vent est fort, moins les méthodes approchées sont précises. On voit cependant que la méthode du temps corrigé reste d’une précision tout à fait opérationnelle même avec des vents assez fort.
(Le graphique suppose que le vent est dans l’axe de la route, soit de face, soit de dos. )
Ci-dessous mon dernier vol, qui vous montre que le vent peut être très fort, et presque dans l’axe…

130kt de vent de face à l’aller,
107 kt de composante favorable au retour.
À l’aller, la vitesse propre Vp était d’environ 273kt dans les conditions du moment. L’angle au vent était si faible qu’on peut considérer que cos θ= 1
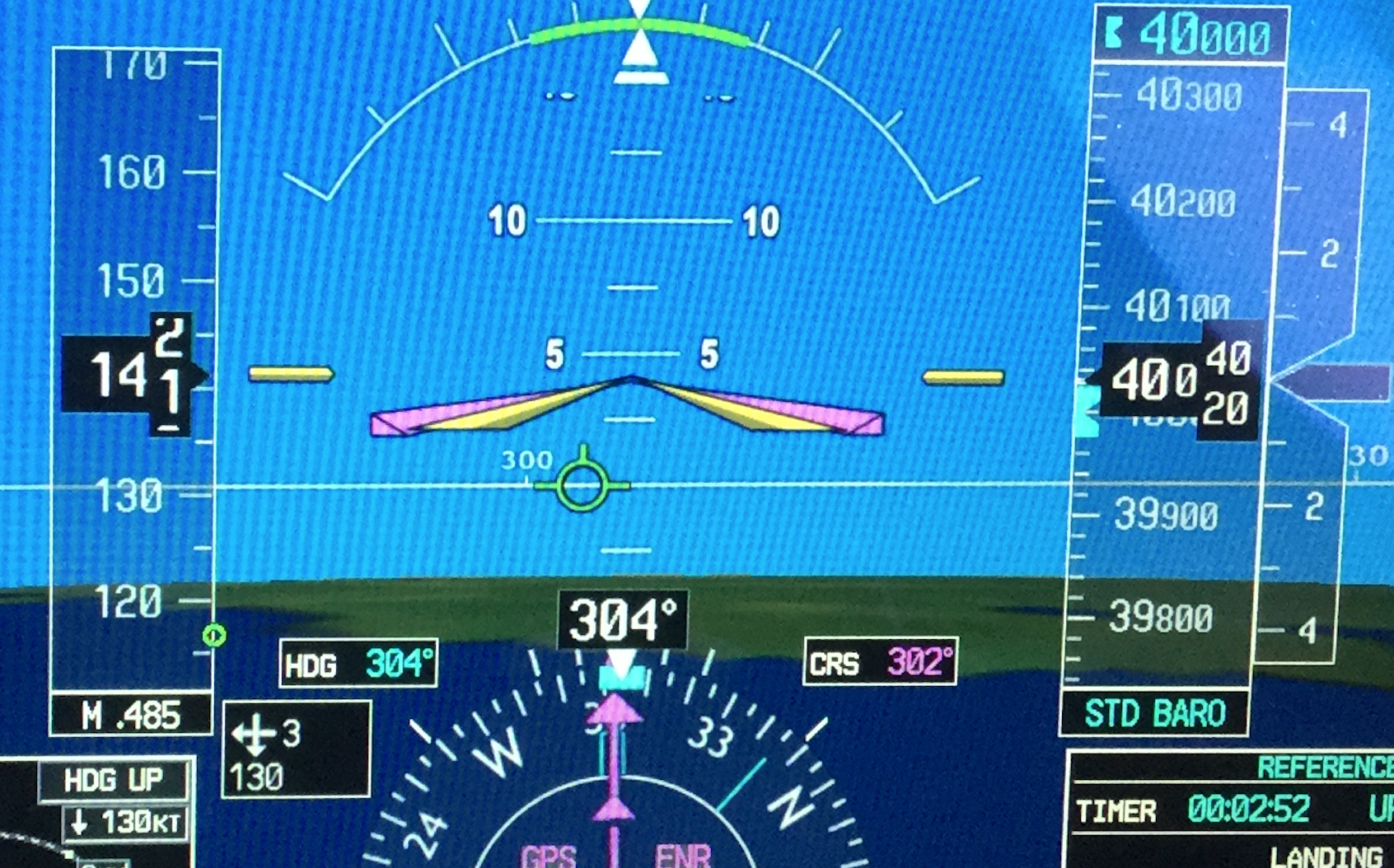
Fb {=\frac{60}{V_p}= \frac{60}{273}}=0.2
Xm=Fb x W = 0.2 x 130 = 26°
t=Xm cos θ = 26 x 1 = 26
t″{=\frac{t^2}{60}= \frac{26^2}{60}= \frac{676}{60}}=11.
Soit tc26+11=37 mn de plus par heure de vol, pour un résultat réel de {60 . ( \frac{273}{273-130}-1 )}=55mn.
Vous constatez qu’avec un vent très fort, les formules enseignées ne peuvent plus être utilisées. Cependant ces situations sont exceptionnelles. De plus la photographie de l’aller a été prise au moment où l’avion atteignait son altitude de croisière et n’avait pas encore accéléré à sa vitesse propre de croisière.
Enfin, ne soyez pas affolé par l’idée d’élever au carré et de diviser par 60 de tête. Vous savez que 252 fait 625. Vous savez que 625/60 fait un peu plus de 10. Donc votre résultat réel sera d’un peu plus de 10, soit 11. Et même si vous vous trompez de quelques unités, ce ne sera pas très important, l’important étant de faire les corrections dans le bon sens.
Un dernier exemple qui anticipe sur le prochain article qui traitera de l’attente: vous êtes dans un avion aussi bien équipé que celui de mon dernier vol, qui vous indique une composante de vent de face de 25kt, votre vitesse propre est de 150kt et vous souhaitez parcourir en une minute la distance que vous auriez parcourue sans vent. Fb=60/150= 0.4, t= 25 x 0.4 = 10 secondes, t″= 102/60=100/60=2 (on arrondi vers le haut si le vent est de face). Le résultat est donc 1mn12 secondes, c’est la valeur exacte(60×150/125), notre arrondi a corrigé l’erreur due à notre approximation. Avec le vent de dos, la méthode vous donne 60- (10 -1) =51 secondes (on arrondi vers le bas avec un vent favorable), pour une valeur exacte de 60×150/175= 51.4 secondes. On peut trouver plus simple de calculer directement, mais je me devais de vous exposer la méthode qui est encore largement enseignée.

Triangle des vitesses

Le schéma est extrait d’un document dénommé Calcul mental : triangle des vitesses, librement disponible sur le site de l’ACAT. L’angle entre la route et le cap est appelé dérive, noté X. X est l’abréviation du mot cross, crosswind voulant dire vent de travers. L’angle entre la route et le vent, noté θ, est appelé angle au vent. La vitesse du vent est notée Vv sur le schéma. Je préfère dans la suite la noter W, W comme wind.
Lors de la préparation d’un vol, j’ai une prévision de vent et j’ai calculé ma vitesse propre (Vp), et j’aimerais connaître, pour préparer ma navigation, la vitesse sol (Vs) et la dérive. Une fois en vol, je pourrai évaluer la dérive et la vitesse sol à l’aide du compas, d’un chronomètre et de repères au sol, ou plus simplement en m’aidant du GPS, et j’aimerais pouvoir en déduire la force et la direction du vent.
Posons les équations reliant toute ces valeurs.
(1){V_p \cos \, X -W \cos \, \theta =V_s }
(2){V_p \sin \, X -W \sin \, \theta =0}
Arrêtons nous un instant sur ces formules pour examiner les conventions que nous avons adoptées. Si l’angle au vent est nul, (2) nous dit que a dérive est nulle, et (1) qu’il faut retrancher le vent de la vitesse propre pour trouver la vitesse sol. Nous adopterons la convention que le vent est toujours positif, qu’un angle au vent inférieur à 90° veut dire qu’on subit une composante de face, et qu’un angle au vent supérieur à 90° veut dire qu’on bénéficie une composante favorable. Le signe de l’angle au vent correspond à un vent de droite ou de gauche, nous considérerons que le signe est toujours positif, et que le vent vient de gauche.
Intéressons nous en premier à la dérive
On déduit de (1) et (2)
(3){ X= \arcsin (\frac{W}{V_p} \sin \theta)}.
Si nous désignons par Wx = W sinθ la composante du vent perpendiculaire à la route, nous obtenons
(4){ X= \arcsin (\frac{W_x}{V_p})}.
Nous avons déjà évoqué la formule {\sin \alpha \simeq \frac{\alpha} {60}}, avec α exprimé en degrés, qui peut s’écrire aussi {\arcsin a \simeq 60 a}, l’angle étant là aussi exprimé en degrés, qui consiste à approcher le sinus par sa corde à 30°. Cette formule approchée donne des valeurs exactes pour les angles 0° et 30°, est très précise entre 0° et 30°, et l’erreur devient significative pour des angles dont le sinus dépasse significativement ½. Si on approche le sinus par cette formule la formule (4) devient
(5){ X\simeq \frac{60}{V_p}W \sin \theta=\frac{60}{V_p}W_x}.
En France et, à ma connaissance, nulle part ailleurs, on définit le facteur de base Fb comme le nombre de minutes qu’il faut pour parcourir un NM. Selon le contexte, il s’agit de parcourir un NM air ou un NM sol. Ici il s’agit d’un NM air. Si la vitesse est exprimée en kt, on donc { F_b= \frac{60}{V_p} }. (5) peut donc s’écrire
(6) X≃Fb.W.sinθ = Fb.Wx
Cette formule est très précise tant que Wx ne dépasse pas la moitié de la vitesse propre. L’erreur est inférieure à 2½° si Wx=0.7 Vp, dépasse 5° si Wx=0.8 Vp, dépasse 10° si Wx=0.9 Vp, et atteint 30° si Wx=Vp, c’est à dire si le vent est plein travers et égale la vitesse propre. Dans ce cas extrême, la dérive est de 90°, alors que la formule approchée donne une dérive de 60°.
Dans la suite, nous considérerons que Wx est toujours suffisament petit pour que (6) puisse s’appliquer.
(3) nous permet sans surprise de déterminer que la dérive maximum, notée Xm, est obtenue lorsque l’angle au vent est de 90°:{ X_m= \arcsin (\frac{W}{V_p})}, d’où on tire
(7)Xm≃Fb.W, et de (6) et (7) on obtient enfin
(8)X≃Xm sinθ, formule donnée par tous les manuels, qui est donc utilisable tant que Wx=W sinθ ne dépasse pas significativement la moitié de la vitesse propre. Je vous conseille maintenant la lecture des documents accessibles par le lien donné en début d’article, qui vous donneront de précieux conseils pratiques sur l’utilisation de cette formule.

De (1) et (2) on peut tirer
(9){ V_s= \sqrt{ (V_p^2- W^2 \sin^2 \theta)}-W \cos \theta}, qui donne la vitesse sol en fonction de la force et direction du vent, et de la vitesse propre. Les manuels appellent vent effectif, que je noterai We=W.cosθ, la composante longitudinale du vent. On peut ainsi écrire (9) en fonction du vent effectif We
(10){ V_s= \sqrt{ (V_p^2- W^2 \sin^2 \theta)}-W_e}
Le schéma ci-dessus, tiré du document cité en tête de cet article, rend plus parlante la formule alternative
(11)Vs=Vp.cosX-W.cosθ=Vp.cosX-We,
qu’on peut aussi écrire
{ \frac {V_s}{V_p} = \cos X - \frac {W}{V_p}\cos \theta}, ou encore
(12){ \frac {V_s}{V_p} = \cos X - \sqrt{ (\frac {W}{V_p})^2- \sin^2 X}}.
Les manuels proposent la formule
(13)Vs≃Vp-W.cosθ=Vp-We, en considérant implicitement que la dérive est toujours suffisamment petite pour qu’on puisse en négliger le cosinus.
Prenons un exemple typique de voyage à 100kt de vitesse propre avec un vent de 20kt. Si le vent est plein travers, les manuels (13) nous disent que la vitesse sol sera égale à la vitesse propre. Avec du vent de travers, vous devrez mettre le nez dans le vent, et donc votre vitesse sol sera inférieure à votre vitesse propre: vous n’avez pas besoin de faire de trigonométrie pour vous convaincre alors que la formule (13) n’est pas exacte, en en faisant, vous saurez de combien: (5) nous donne une dérive de X≃Fb.W.sinθ = 0.6×20=12°, la différence entre (11) et (13) permet de calculer que l’écart entre l’approximation et la réalité est de 1-cos(12°)≃2% , l’approximation est dans ce cas justifiée. Si le vent est de 50kt, (5) nous donne une dérive de X≃Fb.W.sinθ = 0.6×50=30°, la vitesse propre sera de 100kt x cos(30°)=87kt. Dans ce cas, pour obtenir la vitesse sol, il faut diminuer de 13% la vitesse donnée par l’approximation de la formule (13). Dans le tableau ci-dessous, on trouvera pour différente valeurs de la dérive et du rapport { \frac {W}{V_p}} la proportion, en %, dont il faut diminuer le résultat de la formule (13) pour obtenir une valeur exacte.


{ \frac {W}{V_p}}20%30%40%50%60%70%
Dérive 10°-2%-2%-2%-3%-4%-5%
Dérive 15°–-4%-5%-6%-7%-10%
Dérive 20°––-8%-9%-12%-15%
Dérive 25°–––-13%-16%-21%
Dérive 30°–––-13%-20%-26%
Dérive 35°––––-22%-30%

Par exemple, si le vent est de 30kt et ma vitesse propre de 100kt, si je subis une dérive de 15°, je dois minorer le résultat de la formule (13) de 4% pour trouver la valeur juste.
D’un point de vue pratique, tout le monde utilise la formule (13), mais il faut avoir en tête qu’une forte dérive conduit à surestimer la vitesse propre si on utilise la formule (13), et donc arrondir la vitesse trouvée vers le bas va dans le sens de la sécurité.